Skip to content

Trigonometry is a branch of maths that relies on the relationships between the angles and sides of triangles.

This activity uses trigonometry to estimate the heights of tall objects, by making a simple tool that can measure angles.

Printable downloads

Follow these steps…

You will need: a printout of the protractor template, an A4 sheet of paper, a piece of A6 card, measureing tape, 50cm of string, a hole punch, scissors, sticky tape or glue and either a metal washer, large button, keyring with something on it or another type of small weight that can be tied with string.

  1. Print the protractor template and cut it out. Tape or glue it to a card.
  2. Punch a hole through the centre. Loop the string through the hole, and put the washer onto the string before tying the loop.
  3. Roll the A4 piece of paper so that it’s about 2.5cm in diameter. Tape it in place. Line up the ends of the index card with the paper tube and tape the index card in place.
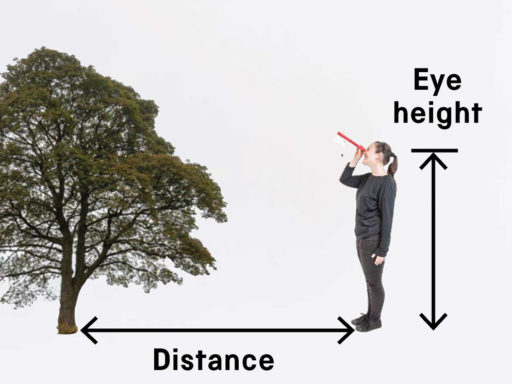  4. Look at the top of something tall through the paper tube.
  5. Move until the string falls at 45 degrees. Now measure the distance to the object along the ground. Add the distance to the height of your eye level, and the result is the object’s height.
  6. Look at something else through the tube. Hold the string where it has fallen and read the angle (θ). Now measure the distance to the object. Use this formula to calculate the height of the object from eye level:

    tan θ x distance to object = object height from eye level

Think and talk about…

  • If you could measure the height of anything, what would it be?
  • How do you think trigonometry could be useful in construction? What about in making video games or in astronomy?

Investigate…

  • Use your height estimator to calculate the height of something. Then measure its actual height with a tape measure. How accurate was your height estimator? Is it more accurate with something that is closer or further away?
  • Try rolling your paper so that it’s smaller or larger in diameter. Do you notice a change?

Did you know?

Trigonometry was used over 2,000 years ago in astronomy to work out the patterns of movement of the Sun, Moon and stars.

What’s the maths?

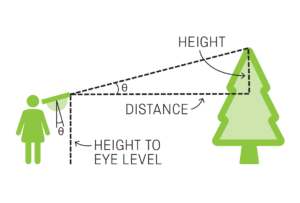In a right-angled triangle in which the other two angles are 45 degrees, two of the sides are equal in length, whatever the size of the triangle. In this activity, the line of sight to the top of a tall object forms the long side (hypotenuse) of such a triangle, making it possible to estimate the height of the object simply by measuring the distance to it and adding the height to your eye level. At different distances, you can work out the height using the tangent function, one of the so-called ‘trigonometric ratios’.

For diagram:

tan θ x distance to object = object height from eye level

object height from eye level + height to eye level = final object height

Maths in your world

This activity makes use of trigonometry – the relationships between the lengths and angles of triangles. Trigonometry has many applications in the real world, in science, engineering and construction. For example, surveyors use instruments called total stations to measure angles and distances before starting construction projects to work out the slope and topography (shape) of the land.