Skip to content

A key mathematical skill is reasoning – making deductions based on logical analysis of available information.

This activity, which involves trying to work out how shoelaces are connected inside a closed tube, provides a fun way to practice and think about logical reasoning.

NOTE

This activity needs to be set up by someone else in advance so that it is a mystery to explore.

Printable downloads

Follow these steps…

You will need: tissue paper or paper, a ruler, sticky tape, a pencil or pen (to make the holes), an observation sheet template, two cardboard tubes (this could be a toilet roll tube, wrapping paper tube, gravy granules container or a poster tube) and shoelaces, ribbon, string or rope (cut four pieces, each twice as long as the tube you are using)

Part one: how to (secretly!) set up the first tube before the activity

  1. Make four holes (two across) in the tube by pushing the pen through it.
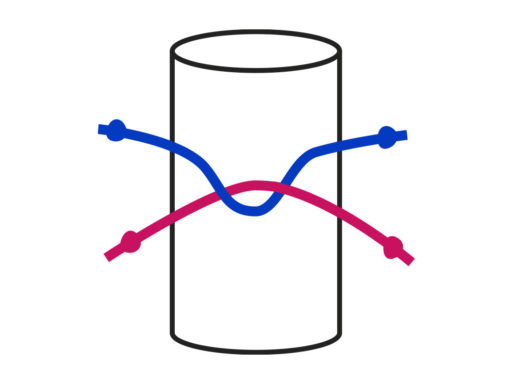  2. Pull two shoelaces through the holes, as shown. Make sure you cross one lace over the other.
  3. Knot the ends of the laces so that they don’t come out. Label the holes A, B, C and D.
  4. Tape paper or plastic over the top and bottom of the tube, so that you can’t see the inside.

Part two: observing the tubes

  1. Without peeking inside, spend some time pulling on the ends of the laces on the mystery tube and see what happens to the other ends.
  2. Keep pulling on the ends and write down all your observations. Try pulling on them in different orders.
  3. Come up with your best idea of how the laces are connected. Draw your best guess on the observation sheet.
  4. Try to replicate how you think the laces are connected in the mystery tube. Use a pen to carefully puncture holes in the tube, and thread the laces through the holes in the way that you think matches the mystery tube.
  5. Test out your best guess. Does the behaviour of your tube match the mystery tube? If it doesn’t, keep testing!
  6. Think about and write down all the different things you’ve done to try and work out the answer – watching the changes, testing different ideas, figuring things out, and so on.

Think and talk about…

  • In maths and science, we won’t always know if we have the correct answer, so we propose a best guess. Does it bother you not knowing for sure that the connections you have guessed for the shoelaces are the correct ones?
  • Why do you think imagination and creativity are so important for maths?
  • How many possible combinations for the laces are there?
  • What skills did you use in this activity? Do you use any of them anywhere else, such as in your hobbies?

Investigate…

Create your own mystery tubes by having the laces connect in a different way – for example, loop them through a button, or have them twist more. Get your friends or family to try and solve the mystery.

Talk to friends, family and people in your local community about the skills they use in their work and everyday life. Use what you discover to reflect on the relevance of skills to maths related work and to other jobs and activities.

Did you know?

Pierre de Fermat made a simple mathematical statement in 1637. It took 384 years before a proof of ‘Fermat’s last theorem’ was worked out using very complicated logical reasoning.

What’s the maths and science?

Attempting to work out what’s going on inside the tube in this activity requires the same kind of reasoning that mathematicians use in solving simple and complex mathematical problems.

Knowledge of the relationships between numbers or shapes allows mathematicians to work out that certain solutions to problems are impossible, and can be ruled out.

Maths in your world

We use logical reasoning when solving even the simplest everyday problems that involve maths – such as dividing a pizza into equal parts or checking a shopping receipt. When faced with these problems we make assumptions, such as 2 + 2 = 4 or dividing a circle with four cuts makes eight pieces. These assumptions are actually based on experience, and on the rules of mathematics, which have been built up over thousands of years.